 |
 |
 |
|
| Fig. 141 | |
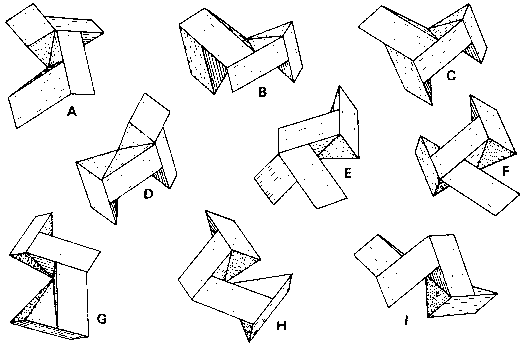
Chapter 9, Fig. 113 shows a rhombic dodecahedron dissected into 12 rhombic pyramids. In the model shown in Fig. 141, each rhombic pyramid is further divided into two identical halves that could be regarded as skewed rhomboid pyramids or triangular stick segments. Not counting side-by-side pairs, there are 10 different ways of joining four such blocks together, analogous to those of the Scrambled Scorpius Puzzle. Nine of these are non-symmetrical and are illustrated in Fig. 141.
Editor's Note: Stewart named this puzzle The Garnet Puzzle.
Problem: from this set of nine pieces, find subsets of six that assemble into the rhombic dodecahedron. Two such subsets are known, and there are probably no others. Either subset makes a satisfactory interlocking puzzle with only one solution and one sliding axis. Five of the pieces are common to both subsets, so an especially interesting version of the puzzle is a set of seven pieces that will construct either solution with one piece set aside.
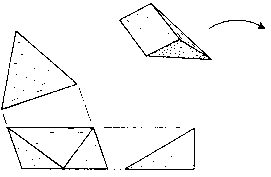
Since this is a fairly easy puzzle to make, the reader is encouraged to do so and discover these two solutions or perhaps experiment with other sizes of pieces and new combinations. The 24 blocks are sawn from 30-60-90-degree triangular cross-section sticks as shown in Fig. 142. If sawn accurately, they tend to align themselves properly when clustered together and held with rubber bands and tape. The desired joints are then glued selectively, one at a time. The finished puzzle, well waxed and with one piece removed, can then be used as a gluing jig for the next one.
Fig. 142
Since the assembled shape of this puzzle is entirely convex, fancy woods can be used and brought to a fine finish by sanding and polishing the 12 outside faces. In combinatorial puzzles of this sort, the addition of multicolor symmetry to an already satisfactory puzzle tends to defeat its purpose. Instead, an attractive random mosaic effect is obtained by making each puzzle piece of a different wood in contrasting colors.
Note also that this is one of the few designs in which all the planes of dissection pass through the center of the puzzle. Consequently, the assembled puzzle can be truncated or rounded down to various sculptural shapes (Fig. 143), making interesting and sometimes surprising patterns in the multicolored versions. By the same token, the assembled puzzle can be either solid or hollow inside.
Fig. 143
The 24-piece dissections of the rhombic dodecahedron and the Scorpius family of puzzles have many characteristics in common, including the fact that one fits exactly inside the hollow center of the other. This suggests the intriguing possibility of a two-tiered puzzle construction. With 48 individual blocks or sticks to work with, the possible puzzle pieces and combinations are practically limitless. Just one example is shown in Figs 144a and 144b. It is made of 48 identical blocks and has the assembled shape of the first stellation of the rhombic dodecahedron, slightly truncated. It may violate the rule that the simplest designs are usually the best, but it does so in such glorious fashion, who cares? Perhaps someone will now be encouraged to try a three-tiered design!
Editor's Note: Stewart named this puzzle The Split Star.
Fig. 144a
Fig. 144b
Now to the other extreme! It has already been shown that polyhedral puzzles need not have many pieces to be interesting and even challenging. The confusing Three-Piece Block Puzzle speaks for itself. The fewest pieces an assembly puzzle can have is, by definition, two. Is it possible to create an interesting assembly puzzle of just two pieces?
When our three children were quite small, they used to spend hours in my workshop patiently gluing together little scraps of fancy woods to make "puzzles" for their friends. One time we had a surplus of truncated rhombic pyramid blocks which they industriously glued together all different ways. What emerged from this was a simple two-piece dissection of the rhombic dodecahedron (Fig. 145). It has two mirror-image halves made of six blocks each that fit together with no difficulty whatsoever. It is when you try to take it apart that the fun begins. If made carefully so that the division of the two halves does not show, nearly everyone will grasp randomly with thumb and forefinger of each hand on opposite faces and pull. But when you do that, you will always be holding both pieces in each hand, and it will never come apart. Only when one uses an unnatural three-finger grasp with each hand and then hunts randomly for the one sliding axis will it come apart with ease!
We made and sold these for a few years. The kids used to put a penny inside, hence the name. I think they used up all the scraps and got interested in other things at about the same time, and production ceased. We tinkered with many variations. The only limit here is your imagination. There are truncated and stellated versions, rounded, three-piece, and multicolored ones. There are nesting sets in which each one is different. A few random samples are shown in Fig. 146.
Fig. 146
One of the most amusing and confusing versions was a matched set of two Pennyhedrons - each one made of 24 tetrahedral blocks, as shown in Fig. 147. One of these is the standard Pennyhedron that comes apart with the tricky three-finger grasp. The other one, which looks exactly the same, comes apart easily along a fourfold axis of symmetry with the common thumb-and-forefinger grasp. Naturally the kids could do the tricky one, but the easy one had them completely baffled! (We will be seeing this dissection again in Chapter 21.)
 |
 |
Fig. 147
| ©1990-2012 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |