All of the puzzles described thus far (except one) have been non-interlocking. Most of them employ a tray or box to hold the pieces in place. The puzzles to be described in this chapter, and throughout the remaining chapters, are interlocking. In other words, they hold themselves together. To be more precise, an interlocking puzzle is here defined as one in which the last step of assembly (or first step of disassembly) necessarily involves sliding of mating surfaces parallel to each other. Such puzzles tend not to come apart without deliberate effort. A box is no longer needed to hold them, so they can be any geometrical shape and can be displayed in full view when assembled. There is more freedom in manipulation of the pieces. Beyond these obvious practical advantages, isn't there something intrinsically more satisfying in things that stay together rather than fall apart by themselves? (Anyone who owns a car like mine will understand!)
The polycube pieces in the previous chapter were formed by joining cubic blocks together different ways. None of the pieces thus formed up to size-five are sufficiently crooked to have much practical use as interlocking puzzle pieces. More importantly, the combinatorial approach does not lend itself very well to the design of interlocking block puzzles.
The most obvious method of designing an interlocking cubic block puzzle is to start with the complete pile of blocks, held loosely together by your imagination or some other means, and remove one piece at a time. A 4 x 4 x 4 cubic pile is a good size for this, with its millions of possible dissections. Depending upon just what the objectives are, quite a bit of experimenting may be required to achieve the desired results. Again, the plastic play blocks that snap together are handy.
A commonly accepted rule for combinatorial puzzle design is that the pieces all be dissimilar and non-symmetrical. The fundamentals of good design also require that the simplest possible pieces be used that will do the job. Given the 4 x 4 x 4 cube then, this translates into maximizing the number of pieces. What is the maximum number of dissimilar non-symmetrical pieces that will assemble into an interlocking 4 x 4 x 4 cube? (Answer unknown.)
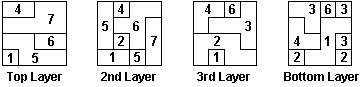
Because of the millions of possible ways of dissecting the 4 x 4 x 4 cube into dissimilar, non-symmetrical, interlocking puzzle pieces, additional aesthetic considerations may be introduced to make the design process more of an art rather than just a series of random choices. The puzzle could be made serially interlocking, meaning that it can be assembled in one order only. Also, by using 1 x 1 x 2 blocks in the construction, symmetrical patterns can be realized on the six outside faces. Shown in Figs. 61a, 61b and 61c (made by Wayne Daniel) is a seven-piece dissection that attempts to achieve all of these. It was once produced as the Convolution Puzzle. It has one surprising step in assembly that requires a rotation, which is not possible unless certain edges are rounded ever so slightly. Can any reader devise a way to correct this mechanically slight but mathematically crippling deformity in an otherwise satisfactory design?

Fig. 61a
Fig. 61b
Fig. 61c
Challenge: join just 10 cubic blocks together to make three puzzle pieces that interlock to form a puzzle having threefold axial symmetry. Impossible? Of course, if you assume that the blocks are joined face-to-face. But when cubic blocks are joined by their half-faces or quarter-faces, many new possibilities arise, as well as hopeless confusion!
All of the information required to construct such a puzzle is contained in the drawings in Fig. 62. This is such an amazing puzzle, it would be a shame to spoil it by giving the solution here. But note the following: interlocking puzzles of this sort must be quite accurately made to be entirely satisfactory or even to be assemblable at all. Usually the easiest way to achieve this is to glue at least some of the joints with the blocks held together in their assembled positions. Since that option is not given here, unless the reader is able to achieve the difficult feat of solving this puzzle on paper, the alternative is to first make a rough model using soft material or rubber cement. Then, after the solution is discovered, a model accurate model can be made of hardwood.
This puzzle has an interesting history. The one symmetrical face of the assembled puzzle happens to resemble a certain corporate logo. The company wanted a simple puzzle incorporating this pattern for some sort of promotional scheme. So the arrangement of six of the blocks was already determined. All that was required to complete the design was the addition of four more blocks in a sort of triangular pyramid and a judicious choice of glue joints to make it into an interesting interlocking puzzle. So the company got what they wanted - except for one thing. It turned out to be anything but simple! Do not be discouraged if you cannot solve it straight away - it has baffled experts!