Puzzles consisting of interlocking assemblies of notched sticks are often referred to as burr puzzles, probably from being pointed or spur-like in assembled appearance. By far the most familiar of all burr puzzles, and probably of three-dimensional puzzles in general, is the so-called six-piece burr. Its origin is unknown, but it has been traced back to at least 1803 in Germany, where it appears in a catalogue of G. H. Bestelmeier. Some persons know it as the Chinese Puzzle or Chinese Cross, probably because it has been mass-produced in the Orient since the early 1900s, but there does not appear to be any evidence that the idea originated there.
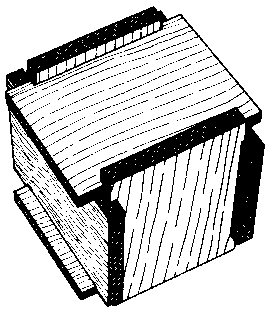
David Bruce has put forth the plausible conjecture that some of the earliest puzzles may have been but slight modifications of practical objects. For example, note the familiar interlocking box shown in Fig. 63, consisting of six notched boards. Did some whimsical box-maker decide to have fun one day in his spare time, or did he perhaps just run out of nails? Whatever, this may well have been the origin of the six-piece burr. With six identical pieces, as suggested by the illustration, it is clearly impossible to assemble. There are several obvious ways to modify one or more of the pieces to make it assemblable, and a good exercise for the amateur puzzle-maker is to see how many of these ways he or she can discover. With a penny slot, it becomes a toy bank - a good first puzzle for any youngster.
Fig. 63
The standard six-piece burr consists of six notched square sticks of arbitrary equal length not less than three times their width, arranged symmetrically in three mutually perpendicular intersecting pairs. If the square cross-section of the sticks has a dimension of two units, then all notches are one unit deep and one unit wide or some exact multiple. To put it another way, all notches can be regarded as being made by removal of discrete cubic units, or to put it still another way, all pieces can be regarded as being built of cubic units. All of the notches are made within the region of intersection with the other sticks, so that when the puzzle is assembled no notches show and it has apparent symmetry (Fig. 64).
Fig. 64
The six-piece burr is actually a large family of designs, since the designer has a wide choice of how to notch each of the pieces. Over the years, variations of the six-piece burr have received much attention from puzzle inventors and authors. Directions for making them can be found in many books and magazines. Several different versions have been manufactured and patented. The earliest US patent is No.1,225,760 of Brown, dated 1917, with several others following shortly thereafter. Most toy and novelty stores have a few burr puzzles on their shelves or in their catalogues. Traditionally, these have been uninspired time-worn versions with sliding key and internal symmetries. Consequently this fine puzzle has suffered a chronically tarnished image. To make matters worse, over the years many inventors have tinkered with bizarre embellishments to give the basic burr puzzle their own stamp of identity. The patent files reveal many such ill-conceived contraptions, including those with strings and holes, hidden pins, rotating keys, and other secret locking devices. Evidently taking their cue from certain composers of modern "music", they have thrown in odd intervals, incongruously sharpened or flattened pieces, confusingly large numbers of parts in hopeless disharmony with each other, and other jarring complications. Within the last decade or two, though, the six-piece burr has emerged from this decadent period to become once again the quintessential interlocking puzzle, thanks largely to the work of Bill Cutler.
There are twelve cubic units in each piece that are candidates for removal (Fig. 65). Removing these in all possible permutations would theoretically result in 4,096 different pieces, but by discarding symmetries and those that cut the pieces in two, the number of practical pieces is 837. No one knows how many different ways sets of six such pieces can be combined and assembled, but they number in the millions. Cutler limited his analysis to only those combinations that make a solid assembly with no internal voids. Using a computer, he found there are 369 usable pieces and they can be assembled into a solid burr 119,979 different ways. These results were published in the Journal of Recreational Mathematics, Vol. 10(4), 1977-78, and were summarized by Martin Gardner in Scientific American, Mathematical Games column, Jan. 1978.
Editor's Note: Bill Cutler continued his analysis of six-piece burrs culminating in the 1994 publication of A Computer Analysis of All 6-Piece Burrs. His analysis showed that there are roughly 35.65 billion possible assemblies (71.3 billion if mirror images are counted). Of these, 35.65 billion assemblies, 5.95 billion can be taken apart. The highest level found for a non-unique (more than one assembly) six-piece burr was 12. The highest level unique six-piece burr is 10 if the pieces are 8 units long and 9 if the pieces are 6 units long. If all pieces are notchable, the highest level is 5 for a unique burr. His analysis completely explored all assemblies for the first piece to be taken out. Only higher level burrs were completely analyzed. So the number of total solvable burrs is a statistical estimate.
Fig. 65
The burr pieces can be divided into two groups - those with simple notches that can be milled out directly with a saw or dado blade (notchable pieces), and those with blind corners and edges that must be chiseled out or made by gluing in cubic blocks (unnotchable pieces). The notchable pieces are the more desirable from both practical and aesthetic considerations. Some puzzle analysts have limited their investigations to notchable pieces, of which there are 59 (including the one with no notches). It has been customary to consider only solid assemblies, in which case there are only 25 usable notchable pieces, and these are commonly referred to as the set of 25 notchable pieces. They can be chosen in sets of six and assembled solid in 314 different ways. Some of this was calculated independently by several different analysts, with or without a computer. All of it has been confirmed and organized by Cutler.
In Fig. 66, piece A is notchable. Piece B is not notchable. Piece C can be made with a saw but cannot be assembled with other notchable pieces without producing voids, so it is not included in the set of 25 notchable pieces, which are shown in Fig. 67.
Fig. 66
Fig 67
Cutler's computer analysis told only what was possible, not what was most interesting. Actually it might possibly have done that too if appropriately instructed. For example, from the list of the 314 solid notchable combinations, suppose one first eliminates all those using duplicates (or triplicates) of identical pieces and pieces having an axis of symmetry. Also eliminate combinations with more than one solution. This narrows the field down to 18, of which all but one (and its mirror image) employ a rather common and uninteresting two-piece key arrangement. What emerges from this screening process is a marvelous burr. It is called Burr No. 305 because of its location in Cutler's tabulation. It uses pieces 6, 12, 14, 21, 22, and 23 (Fig. 68).
Fig. 68
This is an appropriate point at which to digress for a moment and introduce the idea of a difficulty index for a combinatorial puzzle. Puzzles must by definition have some element of difficulty. Making a puzzle more difficult may in some circumstances be an improvement in design, if not carried to extremes and if not to the detriment of other considerations. In any case, some way of predicting the relative difficulty of similar puzzle designs would be a useful tool for the designer.
Consider the solid six-piece burr. Given a drawing of the assembled burr or some familiarity with it, the only real problem is determining the relative location and orientation of the six pieces. Select any one of the six pieces at random for the bottom piece. Usually it is obvious from the notching which side should face the center. Now for the back piece, one has a choice of any of the remaining five, and it can be turned end-for-end, hence a total of ten possibilities. For the next piece, say on the left, there are six choices, and so on. Thus, to make a complete analysis of the puzzle by trying every piece in every position. There are a total of 10 x 8 x 6 x 4 x 2 or 3,840 possibilities to be considered. This number divided by the number of solutions is the difficulty index of that particular design.
The difficulty index of Burr No. 305 is 3,840. While that may seem like a large number of moves, most of them are skipped by using common sense, and so this would be a puzzle of medium difficulty. Identical pairs of pieces, symmetrical pieces, and multiple solutions all decrease the difficulty index. There is one charming type of piece known as an ambiguous piece, because you cannot tell from the notches which side should face the center, and there are different degrees of ambiguity. Piece No. 9 in Fig. 67 is an example of the most ambiguous type because any one of its four sides might face the center. This would increase the difficulty index by an additional factor of four, but because it is also symmetrical the net increase would be a factor of two.
The mischievous role of the ambiguous piece was not taken into account in the analysis that led to the illumination of Burr No. 305. Adding this newfound ingredient to the recipe another delectable puzzle comes to light - Burr No. 306 illustrated in Fig. 69. It uses pieces 6, 9, 12, 21, 22, and 23, and has a difficulty index of 7,680.
Note that a set of seven pieces will allow both Burr No. 305 and Burr No. 306 to be constructed.
Fig. 69
So far we have discussed only burrs with no internal voids. Historically, solid burrs have received the most attention. No satisfactory explanation has ever been given for this, but perhaps it is simply the notion that many things in life tend to be more satisfying when they are solid - building foundations, financial investments, friendships, and so on. Also, Bill Cutler points out that only by limiting his program to solid burrs was the analysis practical as otherwise the computation time would have been too long. (Editor's Note: This is no longer true. See the previous note on this subject.) The recent flurry of activity in designing ever more entertaining (meaning, to some, fiendishly difficult) burrs has shifted attention to burrs that do not come directly apart (or go directly together) but rather involve the shifting back and forth of pieces or groups of pieces within the partially assembled burr. Some of these are so baffling as to discourage a professional locksmith yet they are basically just standard burrs using the 837 practical pieces. They all necessarily have one or more internal voids.
One of the best of this new breed of burrs is Bill's Baffling Burr, designed of course by Cutler. It uses two unnotchable pieces, both of which are easily made from notchable pieces by gluing in one and two extra blocks. It has seven internal voids. This is an unusually large number of voids for a burr with only one solution, and contributes to its difficulty, for there are 24 apparent solutions but only one that is possible to assemble. Thus, you may think you have found the solution and are wondering how to get the last piece in place when most likely you have stumbled upon one of the 23 false solutions. It was stated earlier that the pieces could be of arbitrary length. With some of these more complicated burrs, this is no longer true. Bill's Baffling Burr (Fig. 70) cannot be assembled if the pieces are longer than three times their width.
Fig. 70
Bill's Baffling Burr is referred to as a level-five burr, meaning that five separate shifts are required to release the first piece. This new yardstick of devilry has spurred some rivalry among puzzle experts to see who can come up with even higher level burrs. Around 1985, Gaby Games of Israel came out with an amazing level-seven-four burr, meaning that seven moves are required to release the first piece and four more are required to release the second piece. Would someone next discover a level-eight burr? Well, not exactly. Recently Peter Marineau surprised the puzzle world with a level-nine burr! Is this the upper limit? Probably not. The Marineau burr, shown in Fig. 71 achieves its remarkable stunt with surprisingly simple pieces. Two are identical, another two are a reflexive pair, and another one is self-reflexive.
Fig. 71
Perhaps the reader will now be encouraged to wander off into this vast wilderness of hidden notches and explore some of them further. For the puzzle connoisseur, a well-crafted six-piece burr is the embodiment of good design - simple, direct, and eminently functional. For the hobbyist, the burr is well suited for a workshop project and helpful woodworking tips are given later. In particular, the would-be puzzle inventor will find much to explore beneath the deceptively familiar exterior of the six-piece burr.
Considering the large number of possible assemblable sets of the 837 practical pieces, recently estimated by Cutler to almost certainly exceed one billion, any one of them chosen at random is likely to be a new and original, but totally uninspired, design. The first step, then, is to decide just what features one considers most desirable. A few guide-lines have been suggested here, but there may be other, better ideas that have been overlooked. Originality, psychology, and aesthetics all play a role at this stage of the creative process. The second step is seeking the combination that best achieves one's goal, and this is essentially an analytical and mechanical problem.
Imagine a computer being programmed to methodically print out all of the probably billions of assemblable standard six-piece burrs. All but a handful would be new and original designs - or would they? Does merely being different constitute originality? There is a curious musical analogy. With conventional discrete musical notation, one could, in theory at least, program a computer to print out every possible musical theme, given enough time and unlimited supply of paper. Buried within this mountain of papers would be all of the most sublime works of the great masters of the past and of those perhaps to come in the next Renaissance. But then how could they be found from amongst the random noise? The whole exercise would amount to nothing.
Trying to improve upon an existing burr design can be an enlightening exercise. For example, as a maker of puzzles, one is always trying to reduce the number of unnotchable pieces. Moving or removing just one offending unit block seems innocent enough, but it nearly always causes havoc. Attempts to correct the problem just create more problems. (Sounds familiar?) Sometimes you work through a loop of changes and end up back where you started. It is slow work for every new change requires an analysis of all possible solutions. Some analysts use a computer for this. It does in seconds what otherwise might take hours or even days. Others not in such a rush may enjoy the mental exercise in traditional methods of analysis using pencil and paper. For them, the analysis is the puzzle so why not relax and enjoy it?