[Home] [Contents][Figures] [Search] [Help]
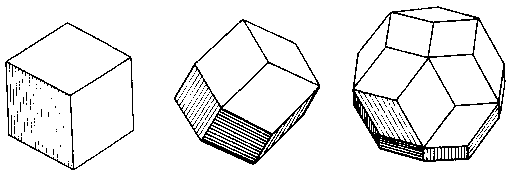
The number of ways that sticks can be arranged symmetrically in space is very limited. It is convenient to examine this question in terms of unnotched straight sticks. The standard six-piece burr can be regarded as a cluster of six rectangular sticks to which parts have been added (or removed) to achieve interlock and other interesting features. The Pin-Hole Puzzle is an even better example. The hollow space in the center is cubic. In any symmetrical arrangement of straight sticks totally enclosing a hollow center, a little thought or experimentation will show that the faces of the enclosed hollow center must be rhombic (or square). There are only three isometrically symmetrical solids with such faces - the cube, the rhombic dodecahedron, and the triacontahedron (Fig. 91).
Fig. 91
The rhombic dodecahedron has 12 identical rhombic faces. It can be visualized as the solid that results when the edges of a cube are sufficiently beveled at 45 degrees (Fig. 92a). It is one of very few symmetrical solids that pack to fill space, two others being the cube and truncated octahedron. Like the cube, it has three fourfold axes of symmetry, four threefold axes, and six twofold axes (Fig. 92b). When viewed along any of its fourfold axes it appears square in profile, while along any of its threefold axes it appears hexagonal (same as the cube).
Fig 92a
Fig. 92b
The rhombic dodecahedron can be totally enclosed by a symmetrical cluster of 12 sticks having equilateral-triangular cross-section, a property not only intriguing but of great practical significance. This arrangement has a pair of mirror-image forms, as shown in Fig. 93.
Fig. 93
At first glance, the nest of sticks shown in Fig. 93 may appear to be self-supporting. Any attempt to assemble it without tape or rubber bands will immediately dispel this notion as the sticks tumble into a heap. A useful tool for the puzzle designer would be some way of analyzing such geometrical arrangements to determine if they are interlocking or not, or even possible to assemble. If the arrangement is totally symmetrical, there is a simple way to do this, as follows:
To take a trivially simple example to start with, consider the Pin-Hole Puzzle without the pins and holes. In its assembled condition as shown (Fig. 94), the two ends of each piece rest flat against two others, and the ends of yet two others rest flat against it. Now move each piece by some incremental distance directly away from the center, and note that they become separated from each other. This is sufficient to show that the structure is non-interlocking and will easily fall apart.
Fig. 94
To take one more trivial example, consider a standard six-piece burr (Fig. 95) made up of six identical pieces like notchable piece no. 2 in Fig. 67. Applying this same test, we see that there is interference between the parts and therefore the burr is impossible to assemble.
Fig. 95
Now for a more practical example, consider the diagonal six-piece burr (Fig. 96). As each piece is moved an incremental distance away from the center, there is neither interference nor separation as the mating faces slide parallel to each other. Therefore it is an assemblable interlocking configuration.
Fig. 96
This useful theory of interlock can be applied most easily by using elementary vector analysis. If the radial movement of one piece is represented by vector A and that of a neighboring piece by vector B, then the relative motion of the two is vector A-B, and any sliding surface in an assemblable interlocking puzzle must be parallel to it. Or make a scale drawing of the puzzle and use methods of descriptive geometry. With a little practice and good spatial perception or a model to work with, most of the assemblies discussed in this book are easy to analyze. Applying this theory to the nest of 12 triangular sticks, it is easy to show that they are non-interlocking.
How might the 12 triangular sticks be made into an interlocking assembly? One way would be to use notched sticks, as in the burr puzzles. That scheme will be considered in Chapter 13. Another way is as follows, instead of leaving the center hollow, imagine it filled solid with a rhombic dodecahedron. Now dissect that rhombic dodecahedron into six identical blocks having the shape of squat octahedra, and use each one of them as a center block for joining the triangular sticks together in pairs, as shown in Fig. 97.
Fig. 97
If the theory of interlock is applied to this new six-piece puzzle configuration, it is found to be an interlocking assembly. It can be slid apart along any one of its four sliding axes, independently or concurrently. Unlike the diagonal burr, it separates into two halves that are quite dissimilar, even though each half is composed of three identical pieces and the completed assembly is symmetrical.
If both ends of all 12 sticks are now cut off at the appropriate angle (Fig. 98), an amazing transformation occurs and the assembly becomes the third stellation or the rhombic dodecahedron. (It is assumed that the reader has some familiarity with polyhedra and stellations. If not, any mathematics library should have a book on the subject.) Remove the equivalent of two tetrahedral blocks more from both ends of the sticks, and lo - the second stellation of the rhombic dodecahedron appears. Many intriguing intermediate forms are also possible by removing the equivalent of only one tetrahedral block, or by removing them selectively from certain ends. The biggest surprise occurs when yet two more tetrahedral units are removed from all the ends, producing the now familiar first stellation again (Fig. 99). Is this not amazing? It can be made not only from six square sticks with ends beveled but also from 12 triangular sticks!
Fig. 98
Fig. 99
Another surprise! Having now seen that the second stellation of the rhombic dodecahedron can be constructed by an interlocking assembly of 12 triangular sticks, would you believe that it too can be constructed (more easily, in fact) by an interlocking assembly of six pieces made from square sticks? Start with 18 six-sided center blocks and join them in threes as shown in Fig. 100 to make six identical puzzle pieces, which assemble into the interesting interlocking polyhedral shape shown.
Fig. 100
Now if V-shaped notches are made at both ends of each puzzle piece in the model shown in Fig. 100 the second stellation is produced, as shown in Fig. 101. As practical matter rather than cut notches in the end blocks, it is easier to form them by gluing two suitable blocks together, both of which are easily made from square stock using the saw jig shown in Fig. 90. These are very useful building blocks and will be used frequently in the next two chapters. One of them is a rhombic pyramid, and the other is a five-sided block having the shape of a skewed triangular prism, hereafter referred to as prism block for short.
All of the above models assemble by first forming two halves of three pieces each and then mating the two halves. Unlike those made with triangular sticks, these two halves are mirror images of each other.
In the second stellation model (Fig. 101), if the 12 rhombic pyramid blocks are omitted, the result is the simple but intriguing puzzle shown in Fig. 102. Its six identical pieces are assembled in the usual way of mating two halves, which in this case are dissimilar. The assembled shape is intermediate between the first and second stellation, and it has the symmetry of a tetrahedron. It serves as the skeleton for many other more complicated puzzles to follow. It will be referred to as the Four Corners Puzzle, the name by which a four-color version of it was once produced.
The Four Corners Puzzle is a good example of an interlocking structure with an intriguing geometry and attractive shape but which is trivially simple as an assembly puzzle. To make it also challenging, the concept of color symmetry is introduced. Imagine the end blocks colored four different colors as indicated in Fig. 103.
Fig. 103
Problem: assemble the above pieces in color symmetry. Advanced problem: discover all the possible ways of assembling these pieces in color symmetry. In order to solve this problem, we must first define exactly what is meant here by color symmetry. When a multicolored polyhedral puzzle is said to be assembled in color symmetry, it meets the following test: choose any color and change it to black. Change all the other colors to white. No matter which color was changed to black, the result is the same, and the black pattern has an axis of symmetry.
The four different ways in which the Four Corners Puzzle can be assembled in color symmetry are represented in Fig. 104 in black and white. The one on the left, in which each "corner" is a solid color, is the easiest and most obvious and is how the puzzle got its name. Each has a pair of solutions.
Fig. 104
Finally, to extract one more bit of recreation from this puzzle, discover the 24 ways of assembling it such that the patterns of all four colors are identical but not symmetrical. You may skip the 3,808 ways that do not have either property. Hint: in general, these color symmetry problems are not the type that one solves by trial and error. One must try to discover the principles involved and the simple rules that transform one solution into another. You may not even need the physical pieces.
Continuing in the same vein, shown in Fig. 105 are the six puzzle pieces for a four-color version of the Second Stellation Puzzle. Can you discover the logic of this coloring scheme? Hint: compare with the previous puzzle. Also note that the coloring produces reflexive pairs, as indicated by the broken line.
Fig. 105
There are several ways of assembling these pieces in color symmetry, as shown in Fig. 106. The simplest and most obvious is with each of the eight hexagonal dimples a solid color, with like colors opposite. Another way is with four triangles of solid color. The most elegant is with four hexagonal rings of solid color intersecting each other around the outside. The other ways are left for the curious reader to discover. Trying to solve all of these fascinating color patterns and being able to switch from one to another can be quite confusing arid entertaining.
Fig. 106
There are many different ways of dissecting the various stellations of the rhombic dodecahedron into six identical interlocking pieces, and no purpose would be served by listing them all. Just one more example will be mentioned in this chapter - a simple dissection of the third stellation that lends itself beautifully to a multicolor puzzle.
The construction of each puzzle piece from a six-sided center block and four triangular stick segments is illustrated in Fig. 107a. When assembled, the puzzle has the appearance of twelve triangular sticks, even though each stick is broken in two, with the two halves belonging to two different puzzle pieces. The pieces are colored as shown. The problem is to assemble the puzzle such that each apparent group of three parallel sticks is one color as shown in Fig. 107b. There are four solutions.
Fig. 107a
Fig. 107b
These are but a few of the many interesting multicolor problems that are possible with puzzles of this sort. For example, the three described above all use four colors. Other possibilities exist using 2, 3, 6, 8, or 12 colors. The woods can be stained or painted different colors, but some of the most beautiful effects are obtained by using brightly-colored exotic woods in their natural state. More multicolor puzzles will be described in later chapters.
| ©1990-2012 by Stewart T. Coffin For questions or comments regarding this site, contact the chief metagrobologist: |